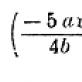Главная » Педагогика » Возведение в степень. Возведение в степень: правила, примеры Степень суммы двух чисел

Возведение в степень. Возведение в степень: правила, примеры Степень суммы двух чисел

Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно - разность квадратов! Получаем:

Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.

Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках.

Но важно запомнить: меняются все знаки одновременно !

Вернемся к примеру:

И снова формула:

Целыми мы называем натуральные числа, противоположные им (то есть взятые со знаком « ») и число.

целое положительное число , а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе.

А теперь давайте рассмотрим новые случаи. Начнем с показателя, равного.

Любое число в нулевой степени равно единице :

Как всегда, зададимся вопросом: почему это так?

Рассмотрим какую-нибудь степень с основанием. Возьмем, например, и домножим на:

Итак, мы умножили число на, и получили то же, что и было - . А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на. Значит.

Можем проделать то же самое уже с произвольным числом:

Повторим правило:

Любое число в нулевой степени равно единице.

Но из многих правил есть исключения. И здесь оно тоже есть - это число (в качестве основания).

С одной стороны, в любой степени должен равняться - сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, как и любое число в нулевой степени, должен равняться. Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.

Поехали дальше. Кроме натуральных чисел и числа к целым относятся отрицательные числа. Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:

Отсюда уже несложно выразить искомое:

Теперь распространим полученное правило на произвольную степень:

Итак, сформулируем правило:

Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: (т.к. на делить нельзя).

Подведем итоги:

I. Выражение не определено в случае. Если, то.

II. Любое число в нулевой степени равно единице: .

III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: .

Задачи для самостоятельного решения:

Ну и, как обычно, примеры для самостоятельного решения:

Разбор задач для самостоятельного решения:

Знаю-знаю, числа страшные, но на ЕГЭ надо быть готовым ко всему! Реши эти примеры или разбери их решение, если не смог решить и ты научишься легко справляться с ними на экзамене!

Продолжим расширять круг чисел, «пригодных» в качестве показателя степени.

Теперь рассмотрим рациональные числа. Какие числа называются рациональными?

Ответ: все, которые можно представить в виде дроби, где и - целые числа, причем.

Чтобы понять, что такое «дробная степень» , рассмотрим дробь:

Возведем обе части уравнения в степень:

Теперь вспомним правило про «степень в степени» :

Какое число надо возвести в степень, чтобы получить?

Эта формулировка - определение корня -ой степени.

Напомню: корнем -ой степени числа () называется число, которое при возведении в степень равно.

То есть, корень -ой степени - это операция, обратная возведению в степень: .

Получается, что. Очевидно, этот частный случай можно расширить: .

Теперь добавляем числитель: что такое? Ответ легко получить с помощью правила «степень в степени»:

Но может ли основание быть любым числом? Ведь корень можно извлекать не из всех чисел.

Никакое!

Вспоминаем правило: любое число, возведенное в четную степень - число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!

А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение не имеет смысла.

А что насчет выражения?

Но тут возникает проблема.

Число можно представить в виде дргих, сократимых дробей, например, или.

И получается, что существует, но не существует, а ведь это просто две разные записи одного и того же числа.

Или другой пример: раз, то можно записать. Но стоит нам по-другому записать показатель, и снова получим неприятность: (то есть, получили совсем другой результат!).

Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем .

Итак, если:

— натуральное число;
— целое число;

Примеры:

Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:

5 примеров для тренировки

Разбор 5 примеров для тренировки

1. Не забываем об обычных свойствах степеней:

2. . Здесь вспоминаем, что забыли выучить таблицу степеней:

ведь - это или. Решение находится автоматически: .

Ну а теперь - самое сложное. Сейчас мы разберем степень с иррациональным показателем .

Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением

Ведь по определению иррациональные числа - это числа, которые невозможно представить в виде дроби, где и - целые числа (то есть, иррациональные числа - это все действительные числа кроме рациональных).

При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.

Например, степень с натуральным показателем - это число, несколько раз умноженное само на себя;

...число в нулевой степени - это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось - поэтому результатом является только некая «заготовка числа», а именно число;

...степень с целым отрицательным показателем - это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.

Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель - это даже не действительное число.

Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.

КУДА МЫ УВЕРЕНЫ ТЫ ПОСТУПИШЬ! (если научишься решать такие примеры:))

Например:

Реши самостоятельно:

Разбор решений:

1. Начнем с уже обычного для нас правила возведения степени в степень:

Теперь посмотри на показатель. Ничего он тебе не напоминает? Вспоминаем формулу сокращенного умножения разность квадратов:

В данном случае,

Получается, что:

Ответ: .

2. Приводим дроби в показателях степеней к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например:

Ответ: 16

3. Ничего особенного, применяем обычные свойства степеней:

ПРОДВИНУТЫЙ УРОВЕНЬ

Определение степени

Степенью называется выражение вида: , где:

— основание степени;
— показатель степени.

Степень с натуральным показателем {n = 1, 2, 3,...}

Возвести число в натуральную степень n — значит умножить число само на себя раз:

Степень с целым показателем {0, ±1, ±2,...}

Если показателем степени является целое положительное число:

Возведение в нулевую степень :

Выражение неопределенное, т.к., с одной стороны, в любой степени - это, а с другой - любое число в -ой степени - это.

Если показателем степени является целое отрицательное число:

(т.к. на делить нельзя).

Еще раз о нулях: выражение не определено в случае. Если, то.

Примеры:

Степень с рациональным показателем

— натуральное число;
— целое число;

Примеры:

Свойства степеней

Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.

Посмотрим: что такое и?

По определению:

Итак, в правой части этого выражения получается такое произведение:

Но по определению это степень числа с показателем, то есть:

Что и требовалось доказать.

Пример : Упростите выражение.

Решение : .

Пример : Упростите выражение.

Решение : Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием мы объединяем, а остается отдельным множителем:

Еще одно важное замечание: это правило - только для произведения степеней !

Ни в коем случае нелья написать, что.

Так же, как и с предыдущим свойством, обратимся к определению степени:

Перегруппируем это произведение так:

Получается, что выражение умножается само на себя раз, то есть, согласно определению, это и есть -я степень числа:

По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: !

Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать? Но это неверно, ведь.

Степень с отрицательным основанием.

До этого момента мы обсуждали только то, каким должен быть показатель степени. Но каким должно быть основание? В степенях с натуральным показателем основание может быть любым числом .

И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже. Давайте подумаем, какие знаки (« » или « ») будут иметь степени положительных и отрицательных чисел?

Например, положительным или отрицательным будет число? А? ?

С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.

Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть, или. Но если мы умножим на (), получится - .

И так до бесконечности: при каждом следующем умножении знак будет меняться. Можно сформулировать такие простые правила:

четную степень, - число положительное .
Отрицательное число, возведенное в нечетную степень, - число отрицательное .
Положительное число в любой степени - число положительное.
Ноль в любой степени равен нулю.

Определи самостоятельно, какой знак будут иметь следующие выражения:

1.	2.	3.
4.	5.	6.

Справился? Вот ответы:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.

В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание - степень четная, а значит, результат всегда будет положительным. Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Очевидно нет, так как (потому что).

Пример 6) уже не так прост. Тут нужно узнать, что меньше: или? Если вспомнить, что, становится ясно, что, а значит, основание меньше нуля. То есть, применяем правило 2: результат будет отрицательным.

И снова используем определение степени:

Все как обычно - записываем определение степеней и, делим их друг на друга, разбиваем на пары и получаем:

Прежде чем разобрать последнее правило, решим несколько примеров.

Вычисли значения выражений:

Решения :

Получаем:

Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило 3. Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.

Если домножить его на, ничего не поменяется, верно? Но теперь получается следующее:

Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках. Но важно запомнить: меняются все знаки одновременно! Нельзя заменить на, изменив только один неугодный нам минус!

Вернемся к примеру:

И снова формула:

Итак, теперь последнее правило:

Как будем доказывать? Конечно, как обычно: раскроем понятие степени и упростим:

Ну а теперь раскроем скобки. Сколько всего получится букв? раз по множителей - что это напоминает? Это не что иное, как определение операции умножения : всего там оказалось множителей. То есть, это, по определению, степень числа с показателем:

Пример:

Степень с иррациональным показателем

В дополнение к информации о степенях для среднего уровня, разберем степень с иррациональным показателем. Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением - ведь по определению иррациональные числа - это числа, которые невозможно представить в виде дроби, где и - целые числа (то есть, иррациональные числа - это все действительные числа, кроме рациональных).

При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах. Например, степень с натуральным показателем - это число, несколько раз умноженное само на себя; число в нулевой степени - это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось - поэтому результатом является только некая «заготовка числа», а именно число; степень с целым отрицательным показателем - это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.

Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.

Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель - это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.

Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)

Например:

Реши самостоятельно:

Ответы:

Вспоминаем формулу разность квадратов. Ответ: .
Приводим дроби к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например: .
Ничего особенного, применяем обычные свойства степеней:

КРАТКОЕ ИЗЛОЖЕНИЕ РАЗДЕЛА И ОСНОВНЫЕ ФОРМУЛЫ

Степенью называется выражение вида: , где:

Степень с целым показателем

степень, показатель которой — натуральное число (т.е. целое и положительное).

Степень с рациональным показателем

степень, показатель которой — отрицательные и дробные числа.

Степень с иррациональным показателем

степень, показатель которой — бесконечная десятичная дробь или корень.

Свойства степеней

Особенности степеней.

Отрицательное число, возведенное в четную степень, - число положительное .
Отрицательное число, возведенное в нечетную степень, - число отрицательное .
Положительное число в любой степени - число положительное.
Ноль в любой степени равен.
Любое число в нулевой степени равно.

ТЕПЕРЬ ТЕБЕ СЛОВО...

Как тебе статья? Напиши внизу в комментариях понравилась или нет.

Расскажи о своем опыте использования свойств степеней.

Возможно у тебя есть вопросы. Или предложения.

Напиши в комментариях.

И удачи на экзаменах!

можно найти с помощью умножения. Например: 5+5+5+5+5+5=5х6. О таком выражении говорят, что сумму равных слагаемых свернули в произведение. И наоборот, если читать это равенство справа налево, получаем, что мы развернули сумму равных слагаемых. Аналогично можно сворачивать произведение нескольких равных множителей 5х5х5х5х5х5=5 6 .

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».

Выражение 5 6 - это степенью числа, где:

5 - основание степени;

6 - показатель степени.

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

В общем виде степень с основанием "a" и показателем "n" записывается так

Возвести число a в степень n - значит найти произведение n множителей, каждый из которых равен а

Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1

Если возвести число «а» возвести в первую степень , то получим само число a: a 1 = a

Если возвести любое число в нулевой степень , то в результате вычислений получим один. a 0 = 1

Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа , третью - кубом этого числа.

В степень можно возводить любое число - положительное, отрицательное или нуль. При этом не пользуются следующими правилами:

При нахождении степени положительного числа получается положительное число .

При вычислениях нуля в натуральной степени получаем ноль.

х m · х n = х m + n

например: 7 1.7 · 7 - 0.9 = 7 1.7+(- 0.9) = 7 1.7 - 0.9 = 7 0.8

Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем :

х m / х n = х m — n , где, m > n,

например: 13 3.8 / 13 -0.2 = 13 (3.8 -0.2) = 13 3.6

При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.

(у m ) n = у m · n

например: (2 3) 2 = 2 3·2 = 2 6

(х · у) n = х n · у m ,

например:(2·3) 3 = 2 n · 3 m ,

При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби

(х / у) n = х n / у n

например: (2 / 5) 3 = (2 / 5) · (2 / 5) · (2 / 5) = 2 3 / 5 3 .

Последовательность выполнения расчетов при работе с выражениями содержащими степень.

При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.

Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.

Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.

Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an = an .

Например, а=2, n=3: 2 * 2 * 2=2^3 = 8 .

Вообще возведение в степень часто используется в различных формулах по математике и физике. Эта функция имеет более научное предназначение, чем четыре основные: Сложение , Вычитание , Умножение , Деление .

Возведение числа в степень

Возведение числа в степень – операция не сложная. Оно связано с умножением подобно связи умножения и сложения. Запись an – краткая запись n-ого количество чисел «а» умноженных друг на друга.

Рассмотри возведение в степень на самых простых примерах, переходя к сложным.

Например, 42. 42 = 4 * 4 = 16 . Четыре в квадрате (во второй степени) равно шестнадцати. Если вам не понятно умножение 4 * 4 , то читайте нашу стать об умножении .

Рассмотрим еще одни пример: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 . Пять в кубе (в третьей степени) равно ста двадцати пяти.

Еще один пример: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729 . Девять в кубе равняется семи сотням двадцати девяти.

Формулы возведения в степень

Чтобы грамотно возводить в степень нужно помнить и знать формулы, указанные ниже. В этом нет ничего сверх естественного, главное понять суть и тогда они не только запомнятся, но и покажутся легкими.

Возведение одночлена в степень

Что из себя представляет одночлен? Это произведение чисел и переменных в любом количестве. Например, двух – одночлен. И вот именно о возведении в степень таких одночленов данная статья.

Пользуясь формулами возведения в степень вычислить возведение одночлена в степень будет не трудно.

Например, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6 ; Если возводить одночлен в степень, то в степень возводится каждая составная одночлена.

Возводя в степень переменную уже имеющую степень, то степени перемножаются. Например, (x^2)^3 = x^(2 * 3) = x^6 ;

Возведение в отрицательную степень

Отрицательная степень – обратное число. Что такое обратное число? Любому числу Х обратным будет 1/X. То есть Х-1=1/X. Это и есть суть отрицательной степени.

Рассмотрим пример (3Y)^-3:

(3Y)^-3 = 1/(27Y^3).

Почему так? Так как в степени имеется минус, то просто переносим в знаменатель данное выражение, а затем возводим в его в третью степень. Просто не так ли?

Возведение в дробную степень

Начнем рассмотрение вопрос на конкретном примере. 43/2. Что означает степень 3/2? 3 – числитель, означает возведение числа (в данном случае 4) в куб. Число 2 – знаменатель, это извлечение корня второй степени из числа (в данном случае 4).

Тогда получаем квадратный корень из 43 = 2^3 = 8 . Ответ: 8.

Итак, знаменатель дробной степени может быть, как 3, так и 4 и до бесконечности любым числом и это число определяет степень квадратного корня, извлекаемого из заданного числа. Конечно же, знаменатель не может быть равным нулю.

Возведение корня в степень

Если корень возводится в степень, равной степени самого корня, то ответом будет подкоренное выражение. Например, (√х)2 = х. И так в любом случае равенства степени корня и степени возведения корня.

Если (√x)^4. То (√x)^4=x^2. Чтобы проверить решение переведем выражение в выражение с дробной степенью. Так как корень квадратный, то знаменатель равен 2. А если корень возводится в четвертую степень, то числитель 4. Получаем 4/2=2. Ответ: x = 2.

В любом случае лучший вариант просто перевести выражение в выражение с дробной степенью. Если не будет сокращаться дробь, значит такой ответ и будет, при условии, что корень из заданного числа не выделяется.

Возведение в степень комплексного числа

Что такое комплексное число? Комплексное число – выражение, имеющее формулу a + b * i; a, b – действительные числа. i – число, которое при возведение в квадрат дает число -1.

Рассмотрим пример. (2 + 3i)^2.

(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.

Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Возведение в степень онлайн

С помощью нашего калькулятора, Вы сможете посчитать возведение числа в степень:

Возведение в степень 7 класс

Возведение в степень начинают проходить школьники только в седьмом классе.

Например, а=2, n=3: 2 * 2 * 2 = 2^3 = 8 .

Примеры для решения:

Возведение в степень презентация

Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.

Итог

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше - записывайтесь на наш курс: Ускоряем устный счет - НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

В продолжение разговора про степень числа логично разобраться с нахождением значения степени. Этот процесс получил название возведение в степень . В этой статье мы как раз изучим, как выполняется возведение в степень, при этом затронем все возможные показатели степени – натуральный, целый, рациональный и иррациональный. И по традиции подробно рассмотрим решения примеров возведения чисел в различные степени.

Навигация по странице.

Что значит «возведение в степень»?

Начать следует с объяснения, что называют возведением в степень. Вот соответствующее определение.

Определение.

Возведение в степень – это нахождение значения степени числа.

Таким образом, нахождение значение степени числа a с показателем r и возведение числа a в степень r – это одно и то же. Например, если поставлена задача «вычислите значение степени (0,5) 5 », то ее можно переформулировать так: «Возведите число 0,5 в степень 5 ».

Теперь можно переходить непосредственно к правилам, по которым выполняется возведение в степень.

Возведение числа в натуральную степень

На практике равенство на основании обычно применяется в виде . То есть, при возведении числа a в дробную степень m/n сначала извлекается корень n -ой степени из числа a , после чего полученный результат возводится в целую степень m .

Рассмотрим решения примеров возведения в дробную степень.

Пример.

Вычислите значение степени .

Решение.

Покажем два способа решения.

Первый способ. По определению степени с дробным показателем . Вычисляем значение степени под знаком корня, после чего извлекаем кубический корень: .

Второй способ. По определению степени с дробным показателем и на основании свойств корней справедливы равенства . Теперь извлекаем корень , наконец, возводим в целую степень .

Очевидно, что полученные результаты возведения в дробную степень совпадают.

Ответ:

Отметим, что дробный показатель степени может быть записан в виде десятичной дроби или смешанного числа, в этих случаях его следует заменить соответствующей обыкновенной дробью, после чего выполнять возведение в степень.

Пример.

Вычислите (44,89) 2,5 .

Решение.

Запишем показатель степени в виде обыкновенной дроби (при необходимости смотрите статью ): . Теперь выполняем возведение в дробную степень:

Ответ:

(44,89) 2,5 =13 501,25107 .

Следует также сказать, что возведение чисел в рациональные степени является достаточно трудоемким процессом (особенно когда в числителе и знаменателе дробного показателя степени находятся достаточно большие числа), который обычно проводится с использованием вычислительной техники.

В заключение этого пункта остановимся на возведении числа нуль в дробную степень. Дробной степени нуля вида мы придали следующий смысл: при имеем , а при нуль в степени m/n не определен. Итак, нуль в дробной положительной степени равен нулю, например, . А нуль в дробной отрицательной степени не имеет смысла, к примеру, не имеют смысла выражения и 0 -4,3 .

Возведение в иррациональную степень

Иногда возникает необходимость узнать значение степени числа с иррациональным показателем . При этом в практических целях обычно достаточно получить значение степени с точностью до некоторого знака. Сразу отметим, что это значение на практике вычисляется с помощью электронной вычислительной техники, так как возведение в иррациональную степень вручную требует большого количества громоздких вычислений. Но все же опишем в общих чертах суть действий.

Чтобы получить приближенное значение степени числа a с иррациональным показателем , берется некоторое десятичное приближение показателя степени , и вычисляется значение степени . Это значение и является приближенным значением степени числа a с иррациональным показателем . Чем более точное десятичное приближение числа будет взято изначально, тем более точное значение степени будет получено в итоге.

В качестве примера вычислим приближенное значение степени 2 1,174367... . Возьмем следующее десятичное приближение иррационального показателя: . Теперь возведем 2 в рациональную степень 1,17 (суть этого процесса мы описали в предыдущем пункте), получаем 2 1,17 ≈2,250116 . Таким образом, 2 1,174367... ≈2 1,17 ≈2,250116 . Если взять более точное десятичное приближение иррационального показателя степени, например, , то получим более точное значение исходной степени: 2 1,174367... ≈2 1,1743 ≈2,256833 .

Список литературы.

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. МатематикаЖ учебник для 5 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 9 кл. общеобразовательных учреждений.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 - 11 классов общеобразовательных учреждений.
Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Когда число умножается само на себя , произведение называется степенью .

Так 2.2 = 4, квадрат или вторая степень 2-х
2.2.2 = 8, куб или третья степень.
2.2.2.2 = 16, четвёртая степень.

Также, 10.10 = 100, вторая степень 10.
10.10.10 = 1000, третья степень.
10.10.10.10 = 10000 четвёртая степень.

И a.a = aa, вторая степень a
a.a.a = aaa, третья степень a
a.a.a.a = aaaa, четвёртая степень a

Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.

Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель . Это число или буква называется показателем степени или степенью числа. Так, а 2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a 3 означает aaa, то есть здесь a повторяется три раза как множитель.

Показатель первой степени есть 1, но он обычно не записывается. Так, a 1 записывается как a.

Вы не должны путать степени с коэффициентами . Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a. Но a 4 = a.a.a.a

Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква . В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении a x , показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень . Так, b m и d n возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b m = b 3 ; но если m = 5, тогда b m =b 5 .

Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d) 3 есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a 3 + 3a 2 b + 3a 2 d + 3ab 2 + 6abd + 3ad 2 + b 3 + d 3 .

Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель , и этот множитель или делитель есть первоначальным числом, которое возводится в степень.

Так, в ряде aaaaa, aaaa, aaa, aa, a;
или a 5 , a 4 , a 3 , a 2 , a 1 ;
показатели, если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножать на a, мы успешно получим несколько значений.

Tак a.a = a 2 , второй член. И a 3 .a = a 4
a 2 .a = a 3 , третий член. a 4 .a = a 5 .

Если мы начнем слева делить на a,
мы получим a 5:a = a 4 и a 3:a = a 2 .
a 4:a = a 3 a 2:a = a 1

Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.

Так, a:a = a/a = 1. (1/a):a = 1/aa
1:a = 1/a (1/aa):a = 1/aaa.

Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.

Или a 5 , a 4 , a 3 , a 2 , a, 1, 1/a, 1/a 2 , 1/a 3 .

Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.

Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a 3) = a 3 .

Тот же самый план записи может применяться к многочленам . Так, для a + b, мы получим множество,
(a + b) 3 , (a + b) 2 , (a + b), 1, 1/(a + b), 1/(a + b) 2 , 1/(a + b) 3 .

Для удобства используется еще одна форма записи обратных степеней.

Согласно этой форме, 1/a или 1/a 1 = a -1 . И 1/aaa или 1/a 3 = a -3 .
1/aa или 1/a 2 = a -2 . 1/aaaa или 1/a 4 = a -4 .

А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a 0 .

Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать a 4 , a 3 , a 2 , a 1 , a 0 , a -1 , a -2 , a -3 , a -4 .
Или a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .

А ряд только отдельно взятых степеней будет иметь вид:
+4,+3,+2,+1,0,-1,-2,-3,-4.

Корень степени может выражен более чем одной буквой.

Так, aa.aa или (aa) 2 есть второй степенью aa.
И aa.aa.aa или (aa) 3 есть третьей степенью aa.

Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.

Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:

Умножайте величину саму на себя столько раз, сколько указано в степени числа.

Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.

Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.

Четвертая степень a есть a 4 или aaaa. (Art. 195.)
Шестая степень y есть y 6 или yyyyyy.
N-ая степень x есть x n или xxx..... n раз повторенное.

Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.

Tак (ay) 2 =a 2 y 2 ; (ay) 2 = ay.ay.
Но ay.ay = ayay = aayy = a 2 y 2 .
Так, (bmx) 3 = bmx.bmx.bmx = bbbmmmxxx = b 3 m 3 x 3 .

Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.

Пример 1. Четвертая степень dhy есть (dhy) 4 , или d 4 h 4 y 4 .

Пример 2. Третья степень 4b, есть (4b) 3 , или 4 3 b 3 , или 64b 3 .

Пример 3. N-ая степень 6ad есть (6ad) n или 6 n a n d n .

Пример 4. Третья степень 3m.2y есть (3m.2y) 3 , или 27m 3 .8y 3 .

Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,

(a + b) 1 = a + b, первая степень.
(a + b) 1 = a 2 + 2ab + b 2 , вторая степень (a + b).
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 , третья степень.
(a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 , четвертая степень.

Квадрат a - b, есть a 2 - 2ab + b 2 .

Квадрат a + b + h есть a 2 + 2ab + 2ah + b 2 + 2bh + h 2

Упражнение 1. Найдите куб a + 2d + 3

Упражнение 2. Найдите четвертую степень b + 2.

Упражнение 3. Найдите пятую степень x + 1.

Упражнение 4. Найдите шестую степень 1 - b.

Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.

Если мы умножаем a + h само на себя или a - h само на себя,
мы получаем: (a + h)(a + h) = a 2 + 2ah + h 2 также, (a - h)(a - h) = a 2 - 2ah + h 2 .

Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.

Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.

Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.

Пример 1. Квадрат 2a + b, есть 4a 2 + 4ab + b 2 .

Пример 2. Квадрат ab + cd, есть a 2 b 2 + 2abcd + c 2 d 2 .

Пример 3. Квадрат 3d - h, есть 9d 2 + 6dh + h 2 .

Пример 4. Квадрат a - 1 есть a 2 - 2a + 1.

Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.

Во многих случаях является эффективным записывать степени без умножения.

Так, квадрат a + b, есть (a + b) 2 .
N-ая степень bc + 8 + x есть (bc + 8 + x) n

В таких случаях, скобки охватывают все члены под степенью.

Но если корень степени состоит из нескольких множителей , скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.

Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)] 2 или (a + b) 2 .(c + d) 2 .

Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго - произведением их квадратов. Но они равны друг другу.

Куб a.(b + d), есть 3 , или a 3 .(b + d) 3 .

Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.

Вторая степень (- a) есть +a 2
Третья степень (-a) есть -a 3
Четвёртая степень (-a) есть +a 4
Пятая степень (-a) есть -a 5

Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a 2
И -a.-a = +a 2

Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.

Третья степень a 2 есть a 2.3 = a 6 .

Для a 2 = aa; куб aa есть aa.aa.aa = aaaaaa = a 6 ; что есть шестой степенью a, но третьей степенью a 2 .

Четвертая степень a 3 b 2 есть a 3.4 b 2.4 = a 12 b 8

Третья степень 4a 2 x есть 64a 6 x 3 .

Пятая степень (a + b) 2 есть (a + b) 10 .

N-ая степень a 3 есть a 3n

N-ая степень (x - y) m есть (x - y) mn

(a 3 .b 3) 2 = a 6 .b 6

(a 3 b 2 h 4) 3 = a 9 b 6 h 12

Правило одинаково применяется к отрицательным степеням.

Пример 1. Третья степень a -2 есть a -3.3 =a -6 .

Для a -2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a 6 = a -6

Четвертая степень a 2 b -3 есть a 8 b -12 или a 8 /b 12 .

Квадрат b 3 x -1 , есть b 6 x -2 .

N-ая cтепень ax -m есть x -mn или 1/x .

Однако, здесь надо помнить, что если знак, предшествующий степени есть "-", то он должен быть изменен на "+" всегда, когда степень есть четным числом.

Пример 1. Квадрат -a 3 есть +a 6 . Квадрат -a 3 есть -a 3 .-a 3 , которое, согласно правилам знаков при умножении, есть +a 6 .

2. Но куб -a 3 есть -a 9 . Для -a 3 .-a 3 .-a 3 = -a 9 .

3. N-ая степень -a 3 есть a 3n .

Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n - чётное или нечётное.

Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.

Квадрат a/b есть a 2 /b 2 . Согласно правилу умножению дробей,
(a/b)(a/b) = aa/bb = a 2 b 2

Вторая, третья и n-ая степени 1/a есть 1/a 2 , 1/a 3 и 1/a n .

Примеры двочленов , в которых один из членов является дробью.

1. Найдите квадрат x + 1/2 и x - 1/2.
(x + 1/2) 2 = x 2 + 2.x.(1/2) + 1/2 2 = x 2 + x + 1/4
(x - 1/2) 2 = x 2 - 2.x.(1/2) + 1/2 2 = x 2 - x + 1/4

2. Квадрат a + 2/3 есть a 2 + 4a/3 + 4/9.

3. Квадрат x + b/2 = x 2 + bx + b 2 /4.

4 Квадрат x - b/m есть x 2 - 2bx/m + b 2 /m 2 .

Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени .

Так, в дроби ax -2 /y, мы можем переместить x из числителя в знаменатель.
Тогда ax -2 /y = (a/y).x -2 = (a/y).(1/x 2 = a/yx 2 .

В дроби a/by 3 мы можем переместить у из знаменателя в числитель.
Тогда a/by 2 = (a/b).(1/y 3) = (a/b).y -3 = ay -3 /b.

Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.

Так, ax 3 /b = a/bx -3 . Для x 3 обратным есть x -3 , что есть x 3 = 1/x -3 .

Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.

Так, a/b = 1/ba -1 , or ab -1 .