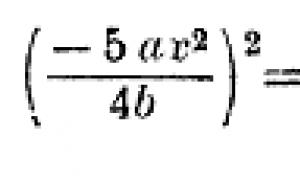Теория галуа. Теория групп и её влияние на различные области математики. Все тела, рассматриваемые в этой главе, считаются коммута-тивными. После К будет называться основным

И очень понравилась. Стиллвелл показывает, как всего на 4-х страницах можно доказать знаменитую теорему о неразрешимости в радикалах уравнений 5-й степени и выше. Идея его подхода в том, что большая часть стандартного аппарата теории Галуа - нормальные расширения, сепарабельные расширения, и особенно "фундаментальная теорема теории Галуа" для этого применения практически не нужны; те их небольшие части, что нужны, можно в упрощенном виде вставить в текст доказательства.

Рекомендую эту статью тем, кто помнит основные начала высшей алгебры (что такое поле, группа, автоморфизм, нормальная подргруппа и фактор-группа), но ни разу не разбирал толком доказательство неразрешимости в радикалах.

Я посидел немного над ее текстом и повспоминал всякие вещи, и все-таки мне кажется, что кое-чего там не хватает, чтобы доказательство было полным и убедительным. Вот как, мне кажется, должен выглядеть план док-ва, в основном по Стиллвеллу, чтобы быть самодостаточным:

1. Надо прояснить, что значит "решить общее уравнение n-ной степени в радикалах". Берем n неизвестных u 1 ...u n , и строим поле Q 0 = Q(u 1 ...u n) рациональных функций от этих неизвестных. Теперь мы можем это поле расширять радикалами: каждый раз добавлять корень какой-то степени от какого-то элемента Q i и получать таким образом Q i+1 (формально говоря, Q i+1 это поле разложения многочлена x m -k, где k в Q i).

Возможно, что после какого-то числа таких расширений мы получим поле E, в котором "общее уравнение" x n + u 1 *x n-1 + u 2 *x n-2 ... будет раскладываться на линейные множители: (x-v 1)(x-v 2)....(x-v n). Иными словами, E будет включать в себя поле разложения "общего уравнения" (оно может быть больше этого поля). В таком случае мы скажем, что общее уравнение разрешимо в радикалах, потому что конструкция полей от Q 0 до E дает общую формулу решения уравнения n-й степени. Можно легко показать это на примерах n=2 или n=3.

2. Пусть есть расширение E над Q(u 1 ...u n), которое включает в себя поле разложения "общего уравнения", и его корни v 1 ...v n . Тогда можно доказать, что Q(v 1 ...v n) изоморфно Q(x 1 ...x n), полю рациональных функций от n неизвестных. Это та часть, которой не хватает в статье Стиллвелла, но есть в стандартных строгих доказательствах. Мы не знаем априори про v 1 ...v n , корни общего уравнения, что они трансцедентны и незасивимы друг от друга над Q. Это надо доказать, и легко доказывается сравнением расширения Q(v 1 ...v n) / Q(u 1 ...u n) с расширением Q(x 1 ...x n) / Q(a 1 ...a n), где a i - симметричные многочлены от x-ов, формализующие то, как коэффициенты уравнения зависят от корней (формулы Виета). Эти два расширения оказываются изоморфными друг другу. Из того, что мы доказали про v 1 ...v n , следует теперь, что любая перестановка v 1 ...v n порождает автоморфизм Q(v 1 ...v n), который таким образом перестанавливает корни.

3. Любое расширение Q(u 1 ...u n) в радикалах, которое включает в себя v 1 ...v n , можно расширить дальше в симметричное относительно v 1 ...v n расширение E". Это просто: каждый раз, когда мы добавляли корень от элемента, который выражается через u 1 ...u n , а значит и через v 1 ...v n (формулы Виета), мы добавляем вместе с ним корни всех элементов, которые получаются любыми перестановками v 1 ...v n . В итоге E" обладает следующим свойством: любая перестановка v 1 ...v n расширяется до автоморфизма Q(v 1 ...v n), который расширяется до автоморфизма E", который при этом фиксирует все элементы Q(u 1 ...u n) (из-за симметричности формул Виета).

4. Теперь мы смотрим на группы Галуа расширений G i = Gal(E"/Q i), т.е. автоморфизмы E", которые фиксируют все элементы Q i , где Q i - промежуточные поля в цепочке расширений радикалами от Q(u 1 ...u n) до E". Стиллвелл показывает, что если добавлять всегда радикалы простой степени, и корни единицы перед другими корнями (несущественные ограничения), то легко видеть, что каждая G i+1 является нормальной подргруппой G i , и их фактор-группа абелева. Цепочка начинается с G 0 = Gal(E"/Q(u 1 ...u n)), и сходит до 1 = Gal(E"/E"), потому что автоморфизм E", фиксирующий E" целиком, есть только один.

5. Мы знаем из пункта 3, что G 0 включает в себя много автоморфизмов - для любой перестановки v 1 ...v n есть автоморфизм в G 0 , расширяющий ее. Легко показать, что если n>4, и G i включает в себя все 3-циклы (т.е. автоморфизмы, расширяющие перестановки v 1 ...v n , которые циклично прокручивают 3 элемента), то и G i+1 включает в себя все 3-циклы. Это противоречит тому, что цепочка заканчивается на 1, и доказывает, что не может быть цепочки расширений радикалами, начинающейся с Q(u 1 ...u n), и включающей в себя в конце поле разложения "общего уравнения".

Теория Галуа

Как было сказано выше, Абель не смог дать общий критерий разрешимости уравнений с числовыми коэффициентами в радикалах. Но решение и этого вопроса не заставило себя долго ждать. Оно принадлежит Эваристу Галуа (1811 -- 1832), французскому математику, скончавшемуся, как и Абель, в очень молодом возрасте. Его жизнь, короткая, но наполненная активной политической борьбой, страстный интерес к математическим занятиям представляют яркий пример того, как в деятельности одаренного человека накопленные предпосылки науки претворяются в качественно новый этап ее развития.

Галуа успел написать мало работ. В русском издании его работы, рукописи и черновые записи заняли лишь 120 страниц в книге маленького формата. Но значение этих работ огромно. Поэтому рассмотрим его замыслы и результаты подробнее.

Галуа обращает в своей работе внимание на случай, когда сравнение не имеет целых корней. Он пишет, что «тогда корни этого сравнения нужно рассматривать как род воображаемых символов, так как они не удовлетворяют требованиям, предъявляемым к целым числам; роль этих символов в исчислении будет часто столь же полезной, как роль воображаемого в обычном анализе». Далее он рассматривает по сути дела конструкцию присоединения к полю корня неприводимого уравнения (явно выделяя требование неприводимости) и доказывает ряд теорем о конечных полях. См [Колмогоров]

Вообще, основная проблема, рассмотренная Галуа,-- это проблема разрешимости в радикалах общих алгебраических уравнений, причем не только в случае уравнений 5-й степени, рассмотренном Абелем. Главной целью Галуа всех исследований Галуа в этой области было найти критерий разрешимости для всех алгебраических уравнений.

В связи с этим, рассмотрим более подробно содержание основной работы Галуа «Мемуар об условиях разрешимости уравнений в радикалах» (Memoiresur les conditions de resolubilite des equations par radicaux.-- J. math, pures et appl., 1846).

Рассмотрим вслед за Галуа уравнение: см [Рыбников]

Для него определим область рациональности -- совокупность рациональных функций от коэффициентов уравнения:

Область рациональности R является полем, т. е. совокупностью элементов, замкнутой по отношению к четырем действиям. Если -- рациональны, то R -- поле рациональных чисел; если же коэффициенты -- произвольные величины, то R есть поле элементов вида:

Здесь числитель и знаменатель -- многочлены. Область рациональности можно расширить, присоединяя к ней элементы, например корни уравнения. Если к этой области присоединить все корни уравнения, то вопрос о разрешимости уравнения делается тривиальным. Задача разрешимости уравнения в радикалах может ставиться только по отношению к определенной области рациональности. Он указывает, что можно изменять область рациональности, присоединяя как известные новые количества.

При этом Галуа пишет: «Мы увидим, сверх того, что свойства и трудности уравнения могут быть сделаны совершенно разными сообразно количествам, которые к нему присоединены».

Галуа доказал, что для всякого уравнения,можно в той же области рациональности найти некоторое уравнение, называемое нормальным. Корни данного уравнения и соответствующего нормального уравнения выражаются друг через друга рационально.

После доказательства этого утверждения следует любопытное замечание Галуа: «Замечательно, что из этого предложения можно заключить, что всякое уравнение зависит от такого вспомогательного уравнения, что все корни этого нового уравнения являются рациональными функциями друг друга»

Анализ замечания Галуа дает нам следующее определение для нормального уравнения:

Нормальное уравнение -- это уравнение, обладающее тем свойством, что все его корни рационально выражаются через один из них и элементы поля коэффициентов.

Примером нормального уравнения будет уравнение: Его корни

Нормальным также будет являться, например, квадратное уравнение.

Стоит,однако, отметить, что Галуа не останавливается на специальном изучении нормальных уравнений, он отмечает только, что такое уравнение «легче решить, чем какое-нибудь другое». Галуа переходит к рассмотрению подстановок корней.

Он говорит что, все подстановки корней нормального уравнения образуют группу G. Это и есть группа Галуа уравнения Q, или, что то же самое, уравнения Она обладает, как выяснил Галуа, замечательным свойством: любое рациональное соотношение между корнями и элементами поля R инвариантно относительно подстановок группы G. Таким образом, Галуа связал с каждым уравнением группу подстановок его корней. Он же ввел (1830) термин «группа» -- адекватное современному, хотя и не столь формализованное определение.

Структура группы Галуа оказалась связанной с задачей разрешимости уравнений в радикалах. Чтобы разрешимость имела место, необходимо и достаточно, чтобы соответствующая группа Галуа была разрешима. Это значит, что в данной группе существует цепочка нормальных делителей с простыми индексами.

Напомним, кстати, что нормальные делители, или, что то же самое, инвариантные подгруппы -- это такие подгруппы группы G, для которых справедливо

где g -- элемент группы G.

Общие алгебраические уравнения при, вообще говоря, такой цепочки не имеют, так как группы подстановок имеют только один нормальный делитель индекса 2 -- подгруппу всех четных подстановок. Поэтому эти уравнения в радикалах, вообще говоря, неразрешимы.(И мы видим связь результата Галуа и результата Абеля.)

Галуа сформулировал следующую фундаментальную теорему:

Для любого наперед заданного уравнения и любой области рациональности существует группа перестановок корней этого уравнения, обладающая тем свойством, что любая рациональная функция -- т.е. функция, построенная с помощью рациональных операций из этих корней и элементов области рациональности, -- которая при перестановках этой группы сохраняет свои числовые значения, имеет рациональные (принадлежащие области рациональности) значения, и обратно: всякая функция принимающая рациональные значения, при перестановках данной группы сохраняет эти значения.

Рассмотрим теперь частный пример, которым занимался еще сам Галуа. Речь идет о том, чтобы найти условия, при которых неприводимое уравнение степени, где простое, разрешимо при помощи двучленных уравнений. Галуа обнаруживает, что условия эти заключаются в возможности так упорядочить корни уравнения, чтобы упомянутая "группа" перестановок задавалась формулами

где может быть равно любому из чисел, а b равняется. Такая группа содержит самое большее p(p -- 1) перестановок. В случае когда??=1 имеется лишь p перестановок, говорят о циклической группе; в общем случае группы называются метациклическими. Таким образом, необходимым и достаточным условием разрешимости неприводимого уравнения простой степени в радикалах является требование, чтобы его группа была метациклической -- в частном случае, циклической группой.

Теперь уже можно обозначить пределы, поставленные сфере действия теории Галуа. Она дает нам некий общий критерий разрешимости уравнений с использованием резольвент, а также указывает путь к их разысканию. Но тут сразу же встает целый ряд дальнейших проблем: найти все уравнения имеющие при данной области рациональности определенную, наперед заданную группу перестановок; исследовать вопрос о том, сводимы ли друг к другу два уравнения такого рода, и если да, то какими средствами и т.д. Все это вместе составляет огромную совокупность проблем, не решенных еще и сегодня. Теория Галуа указывает нам на них, не давая, однако, никаких средств для их решения.

Аппарат, введенный Галуа для установления разрешимости алгебраических уравнений в радикалах, имел значение, выходящее за рамки указанной задачи. Его идея изучения структуры алгебраических полей и сопоставления с ними структуры групп конечного числа подстановок была плодотворной основой современной алгебры. Однако она не сразу получила признание.

Перед роковой дуэлью, оборвавшей его жизнь, Галуа в течение одной ночи сформулировал свои важнейшие открытия и переслал их другу О. Шевалье для публикации в случае трагического исхода. Приведем знаменитое место из письма к О. Шевалье: «Ты публично попросишь Якоби или Гаусса дать их заключение не о справедливости, но о важности этих теорем. После этого будут, я надеюсь, люди, которые найдут свою выгоду в расшифровке всей этой путаницы». При этом Галуа имеет в виду не только теорию уравнений, в этом же письме им сформулированы глубокие результаты из теории абелевых и модулярных функций.

Это письмо было опубликовано вскоре после смерти Галуа, однако идеи, содержащиеся в нем, не нашли отклика. Только через 14 лет, в 1846 г., Лиувилль разобрал и опубликовал все математические работы Галуа. В середине XIX в. в двухтомной монографии Серре, а также в работе Э. Бетти A852), впервые появились связные изложения теории Галуа. И только с 70-х годов прошлого века идеи Галуа начали получать дальнейшее развитие.

Понятие группы в теории Галуа становится мощным и гибким средством. Коши, например, тоже изучал подстановки, но он и не думал приписывать понятию группы подобную роль. Для Коши, даже в поздних его работах 1844--1846 гг. «система сопряженных подстановок» была неразложимым понятием, весьма жестким; он пользовался ее свойствами, но никогда не выявлял понятия подгруппы и нормальной подгруппы. Эта идея относительности, собственное изобретение Галуа, позднее проникла во все математические и физические теории, ведущие свое происхождение от теории групп. Эту идею в действии мы видим, например, в «Эрлангенской программе».(о ней будет рассказано позднее)

Значение работ Галуа состоит в том, что в них в полной мере были раскрыты новые глубинные математические закономерности теории уравнений. После освоения открытий Галуа вид и цели самой алгебры существенно изменились, исчезла теория уравнений -- появилась теория полей, теория групп, теория Галуа. Ранняя смерть Галуа была невозместимой утратой для науки. На заполнение пробелов, понимание и улучшение работ Галуа понадобилось еще несколько десятков лет. Усилиями Кэли, Серре, Жордана и других открытия Галуа были превращены в теорию Галуа. В 1870 г. монографии Жордана «Трактат о подстановках и алгебраических уравнениях» представило эту теорию в систематическом изложении, понятном для всех. С этого момента теория Галуа стала элементом математического образования и фундаментом для новых математических исследований.

Галуа теория, созданная Э. Галуа теория алгебраических уравнений высших степеней с одним малоизвестным, т. е. уравнений вида

устанавливает условия сводимости ответа таких уравнений к ответу цепи др. алгебраических уравнений (в большинстве случаев более низких степеней). Т. к. ответом двучленного уравнения xm = А есть радикал, то уравнение (*) решается в радикалах, в случае если его возможно свести к цепи двучленных уравнений. Все уравнения 2-й, 3-й и 4-й степеней решаются в радикалах. уравнение 2-й степени x2 + px + q = 0 было решено в глубокой древности по общеизвестной формуле

уравнения 3-й и 4-й степеней были решены в 16 в. Для уравнения 3-й степени вида x3 + px + q = 0 (к которому возможно привести всякое уравнение 3-й степени) ответ даётся т. н. формулой Кардано:

опубликованной Дж. Кардано в 1545, не смотря на то, что вопрос о том, отыскана ли она им самим либо же заимствована у др. математиков, нельзя считать в полной мере решенным. Способ ответа в радикалах уравнений 4-й степени был указан Л. Феррари.

В течение трёх последующих столетий математики пробовали отыскать подобные формулы для уравнений 5-й и высших степеней. Самый настойчиво над этим трудились Э. Безу и Ж. Лагранж. Последний разглядывал особенные линейные комбинации корней (т. н резольвенты Лагранжа), и изучал вопрос о том, каким уравнениям удовлетворяют рациональные функции от корней уравнения (*).

В 1801 К. Гаусс создал полную теорию ответа в радикалах двучленного уравнения вида xn = 1, в которой свёл ответ для того чтобы уравнения к ответу цепи двучленных же уравнений низших степеней и дал условия, нужные и достаточные чтобы уравнение xn = 1 решалось в квадратных радикалах. С позиций геометрии, последняя задача заключалась в отыскании верных n-угольников, каковые возможно выстроить при линейки и помощи циркуля; исходя из этого уравнение xn = 1 и именуется уравнением деления круга.

Наконец, в 1824 Н. Абель продемонстрировал, что неспециализированное уравнение 5-й степени (и тем более неспециализированные уравнения высших степеней) не решается в радикалах. Иначе, Абель дал ответ в радикалах одного неспециализированного класса уравнений, содержащего уравнения произвольно высоких степеней, т. н. абелевых уравнений.

Т. о., в то время, когда Галуа начал собственные изучения, в теории алгебраических уравнений было сделано уже большое количество, но неспециализированной теории, охватывающей все вероятные уравнения вида (*), ещё не было создано. К примеру, оставалось: 1) установить нужные и достаточные условия, которым должно удовлетворять уравнение (*) чтобы оно решалось в радикалах; 2) определить по большому счету, к цепи каких более несложных уравнений, хотя бы и не двучленных, возможно сведено ответ заданного уравнения (*) и, например, 3) узнать, каковы нужные и достаточные условия чтобы уравнение (*) сводилось к цепи квадратных уравнений (т. е. дабы корни уравнения возможно было выстроить геометрически посредством линейки и циркуля).

Все эти вопросы Галуа решил в собственном Мемуаре об условиях разрешимости уравнений в радикалах, отысканном в его бумагах по окончании смерти и в первый раз опубликованном Ж. Лиувиллем в 1846. Для решения этих вопросов Галуа изучил глубокие связи между особенностями групп и уравнений подстановок, введя последовательность фундаментальных понятий теории групп. Собственное условие разрешимости уравнения (*) в радикалах Галуа формулировал в терминах теории групп.

Г. т. по окончании Галуа развивалась и обобщалась во многих направлениях. В современном понимании Г. т. - теория, изучающая те либо иные математические объекты на базе их групп автоморфизмов (так, к примеру, вероятны Г. т. полей, Г. т. колец, Г. т. топологических пространств и т. п.).

Лит.: Галуа Э., Произведения, пер. с франц., М. - Л., 1936; Чеботарев Н. Г., Базы теории Галуа, т. 1-2, М. - Л.,1934-37: Постников М. М., Теория Галуа, М., 1963.

Теория Галуа - раздел алгебры, позволяющий переформулировать определенные вопросы теории полей на языке теории групп, делая их в некотором смысле более простыми.

Эварист Галуа сформулировал основные утверждения этой теории в терминах перестановок корней заданного многочлена (с рациональными коэффициентами); он был первым, кто использовал термин «группа» для описания множества перестановок, замкнутого относительно композиции и содержащего тождественную перестановку.

Более современный подход к теории Галуа заключается в изучении автоморфизмов расширения произвольного поля при помощи группы Галуа, соответствующей данному расширению.

Теория Галуа даёт единый элегантный подход к решению классических задач:
Какие фигуры можно построить циркулем и линейкой?
Какие алгебраические уравнения разрешимы с помощью стандартных алгебраических операций (сложение, вычитание, умножение, деление и извлечение корня)?

Более абстрактный подход к теории Галуа был разработан Александром Гротендиком в 1960 году. Этот подход позволяет применить основные результаты теории Галуа к любой категории, обладающей заданными свойствами (например, существованием копроизведений и декартовых квадратов). В частности, это позволяет перенести результаты теории Галуа в теорию накрытий.

Лекции читает Алексей Владимирович Савватеев, доктор физико-математических наук, специалист в области теории игр, ректор Университета Дмитрия Пожарского, доцент ИГУ, популяризатор математики среди детей и взрослых. Работает одновременно в нескольких научных учреждениях, в том числе в Лаборатории исследования социальных отношений и многообразия общества РЭШ. Читает в Яндексе лекции в Школе Анализа Данных, участвует в теоретических исследованиях.

Комментарии: 0

Тони Ротман

Scientific American

В семнадцать лет Галуа многое сделал для создания раздела математики, который ныне даёт возможность проникнуть в сущность таких различных областей, как теория чисел, кристаллография, физика элементарных частиц и возможные позиции кубика Рубика. Известно и то, что в том же возрасте Галуа вторично провалился на экзамене по математике при поступлении в Эколь Политекник (Политехнический институт). Ему пришлось поступить в Эколь Нормаль (Высшую педагогическую школу), но в девятнадцать лет он был оттуда исключён, дважды арестован и заключён в тюрьму за политическую деятельность. Незадолго до дуэли он пережил разочарование в любви; в одном из своих последних писем он, по-видимому, связывает это с дуэлью. «Я умираю, - писал он, - жертвой подлой кокетки».

Алексей Савватеев, Алексей Семихатов

Вопрос науки

Зачем математики придумывают всё новые неразрешимые задачи? Зачем нужна современная математика? Среди ученых нет ни одного, кто разбирался бы во всех областях современных математических наук. А математики придумывают все новые и новые неразрешимые задачи, и потом десятилетиями бьются над ними. Зачем все это? И какое отношение математика имеет к нашей жизни? Гость программы доктор физико-математических наук Алексей Савватеев. Беседует Алексей Семихатов.

И целые числа, и многочлены (от одной переменной с коэффициентами в Q, R или Z/pZ) можно делить с остатком. Эта и подобные аналогии в структуре целых чисел и многочленов играли и продолжают играть важную роль в математике, особенно в теории чисел. В этом курсе мы исследуем такие аналогии в контексте теории чисел: на примере непрерывных дробей, уравнения Пелля, квадратичных вычетов, и abc-гипотезы. От слушателей требуется знакомство с пределами и арифметикой вычетов.

Георгий Шабат

Предполагается прочесть четыре лекции. Первые две будут популярны и общепонятны, а третья и четвёртая будут содержать довольно поверхностные обзоры некоторых перспективных направлений современной математики. 1. О геометрии над конечными полями. 2. Группы Шевалле и группы перестановок. 3. Линейная алгебра над F1 и гомотопическая топология. 4. Разное. Обобщённые кольца Дурова и F∅, F±1, F∞√1. Анализ на множестве корней из единицы (по Хабиро, Концевичу, Манину). О геометрии Аракелова. О тропической математике.

Алексей Савватеев

В миникурсе ликвидируются пробелы школьного образования, относящиеся к теории групп и к конкретным примерам групп. Будут установлены базовые факты про вычеты, доказана малая теорема Ферма, исследованы подгруппы групп перестановок на трёх и четырёх символах, введено понятие нормальной подгруппы данной группы и простоты группы. Затем будет доказано, что группа чётных перестановок на n≥5 символах - простая (что откроет желающим дорогу к вопросам о разрешимости алгебраических уравнений в радикалах), а также что подгруппа переносов плоскости (пространства) - нормальная в группе всех (аффинных) движений соответствующего объекта. Маломерные группы движений получат полную характеризацию (теорема Шаля и законы композиции движений разных видов).

Аркадий Скопенков

Предлагаются наброски элементарных доказательств: теоремы Гаусса о построимости правильных многоугольников; теоремы о неразрешимости уравнений в вещественных радикалах; теорем Руффини-Абеля и Галуа о неразрешимости уравнений в комплексных радикалах. Приводимые доказательства не используют термина «группа Галуа» (даже термина «группа»). Несмотря на отсутствие этого термина, идеи приводимых доказательств являются отправными для теории Галуа (которая вместе с теорией групп развилась из опыта группировки корней многочлена, с помощью которой их можно выразить через радикалы). Приводимые идеи являются отправными также для конструктивной теории Галуа, активно развивающейся в настоящее время.

Алексей Савватеев

Геометрия - классическая Евклидова, Лобачевского, проективная и сферическая - не получает достаточного внимания в программах современных мат.факультетов (не говоря уже о школах). В то же время она наглядна и на редкость красива. Многие утверждения визуально очевидны и в то же время неожиданные (почему самолёт, летящий из Иркутска в Лиссабон, стартует сперва в направлении Норильска?) За 8 лекций слушатели ознакомятся с начальными сведениями в этой области математики, берущей своё начало более двух тысячелетий назад. Закончим мы гораздо более сложным материалом, непосредственно выводящим на современные разделы науки. Будут затронуты основы теории групп и алгебр Ли.

Роман Федоров

Дзета-функция Римана была введена Эйлером в 1737-м году. Она может быть задана рядом ζ(s) = ∑ 1/n^s при тех значениях s, при которых этот ряд сходится. Я буду рассказывать, в основном, об обобщениях дзета-функции Римана - так называемой арифметической дзета-функции, которая ставится в соответствие диофантову уравнению (дзета-функция Римана соответствует «тривиальному» уравнению x=0).

«Одна из задач, над которой работал Эварист Галуа, привлекала внимание математиков в течение долгого времени. Это задача о решении алгебраических уравнений.

Каждому, из нас ещё на школьной скамье приходилось решать уравнения первой и второй степени. Решить уравнение - это значит найти, чему равны его корни. Уже в случае уравнений третьей степени это совсем не так просто. Галуа же изучал самый общий случай уравнения произвольной степени. Каждый из нас может взять лист бумаги, записать такое общее уравнение и обозначить его корни какими-нибудь буквами. Однако эти корни, разумеется, являются неизвестными.

Первое из открытий Галуа состояло в том, что он уменьшил степень неопределенности их значений, т.е. установил некоторые из «свойств» этих корней. Второе открытие связано с методом, использованным Галуа для получения этого результата. Вместо того чтобы изучать само уравнение, Галуа изучал его «группу», или, образно говоря, его «семью».

Понятие группы возникло незадолго до работ Галуа. Но в его время оно существовало как тело, лишённое души, как одно из множества искусственно выдуманных понятий, время от времени возникающих в математике. Революционность того, что сделал Галуа, заключалась не только в том, что он вдохнул в эту теорию жизнь, что его гений придал ей необходимую законченность; Галуа показал плодотворность этой теории, применив её к конкретной задаче о решении алгебраических уравнений. Именно поэтому Эварист Галуа является истинным создателем теории групп.

Группа - это совокупность предметов, имеющих определённые общие свойства. Пусть, например, в качестве таких предметов взяты действительные числа. Общее свойство группы действительных чисел состоит в том, что при умножении любых двух элементов этой группы мы получаем также действительное число. Вместо действительных чисел в качестве «предметов» могут фигурировать изучаемые в геометрии движения на плоскости; в таком случае свойство группы заключается в том, что сумма любых двух движений дает снова движение.

Переходя от простых примеров к более сложным, можно в качестве «предметов» выбрать некоторые операции над предметами. В таком случае основным свойством группы будет то, что композиция любых двух операций также является операцией. Именно этот случай и изучал Галуа. Рассматривая уравнение, которое требовалось решить, он связывал с ним некоторую группу операций (к сожалению, мы не имеем возможности уточнить здесь, как это делается) и доказывал, что свойства уравнения отражаются на особенностях данной группы.

Поскольку различные уравнения могут иметь одну и ту же группу, достаточно вместо этих уравнений рассмотреть соответствующую им группу. Это открытие ознаменовало начало современного этапа развития математики.

Из каких бы «предметов» ни состояла группа: из чисел, движений или операций, - все они могут рассматриваться как абстрактные элементы, не обладающие никакими специфическими признаками. Для того чтобы определить группу, надо только сформулировать общие правила, которые должны выполняться для того, чтобы данную совокупность «предметов» можно было назвать группой. В настоящее время математики называют такие правила групповыми аксиомами, теория групп состоит в перечислении всех логических следствий из этих аксиом. При этом последовательно обнаруживаются все новые и новые свойства; доказывая их, математик всё более и более углубляет теорию. Существенно, что ни сами предметы, ни операции над ними никак не конкретизируются. Если после этого при изучении какой-нибудь частной задачи приходится рассмотреть некоторые специальные математические или физические объекты, образующие группу, то, исходя из общей теории, можно предвидеть их свойства. Теория групп, таким образом, дает ощутимую экономию в средствах; кроме того, она открывает новые возможности применения математики в исследовательской работе.

«Я умоляю моих судей по крайней мере прочесть эти несколько страниц», - так начал Галуа свой знаменитый мемуар. Если бы у его судей хватило гражданского мужества, мы простили бы им недостаток проницательности: идеи Галуа были настолько глубоки и всеобъемлющи, что в то время их действительно трудно было оценить какому бы то ни было учёному.

Множество умов упорно пыталось определить, в чём состоит гениальность. Попытки оказались тщетными, потому что это качество рассматривалось как некое метафизическое явление независимо от обстоятельств, в каких оно проявлялось. На самом же деле гениальность Паскаля , например, не в том, что он мог в двенадцать лет воспроизвести первые тридцать два предложения Евклида , и даже не в том, что после знакомства с Дезаргом он написал работу о конических сечениях. Гениальность Паскаля в том, что он открыл новые, неизвестные раньше связи между различными разделами науки: «Пусть не говорят, что я не сделал ничего нового. Новое - в расположении материала. Когда двое играют в лапту, оба пользуются одним и тем же мячом. Но один из них находит для него лучшее положение». (Паскаль. Предисловие к «Мыслям»). Настоящий исследователь открывает в первую очередь не новые объекты, а новые связи между ними.

Пока нет необходимости, гений молчит. Эту мысль легко подтвердить, стоит только распространить на ученых то, что говорят обычно о государственных деятелях, когда хотят показать, чем они отличаются от людей, вообще занимающихся политикой. Государственный деятель первым замечает изменения, возникшие в соотношении мировых сил; он первым осознает необходимость реагировать на происходящее и в соответствии с этим выбирает для своих действий ту или иную форму. То же самое и в науке. Гениальность ученого проявляется тогда, когда возникает необходимость в каких-то коренных изменениях. Процесс развития человеческих знаний происходит неравномерно. Иногда в той или иной области движение вперед временно прерывается. Наука дремлет в оцепенении. Учёные занимаются мелочами, за красивыми вычислениями скрываются убогие мысли. В начале XIX века алгебраические преобразования так усложнились, что практически движение вперёд оказалось невозможным.

Аппарат, придуманный Декартом и усовершенствованный его последователями, убил то, во имя чего он был создан. Математики перестали «видеть». Даже Лагранж оказался не в состоянии сдвинуть с мертвой точки задачу о решении алгебраических уравнений (это удалось сделать Галуа). Бессилие Лагранжа - яркий пример упадка, переживаемого в то время алгеброй. Настал момент, когда необходимо было найти новые пути. Этот момент определил отнюдь не случай, его вызвала к жизни необходимость. И отличительная черта гения в том, чтобы уловить эту необходимость и немедленно на нее откликнуться.

«В математике, как в любой другой науке, - писал Галуа, - есть вопросы, требующие решения именно в данный момент. Это те насущные проблемы, которые захватывают умы передовых мыслителей независимо от их собственной воли и сознания». История человеческих знаний сохранила имена ученых, сумевших благодаря особой пытливости ума вовремя почувствовать неотложность решительных изменений и указать на это своим современникам. Наука высоко чтит и тех, кто осуществил необходимые перемены. Иногда, хотя и редко, одному человеку удавалось сделать и то и другое. Таким человеком был Лавуазье , таким был и Эварист Галуа.

Имя Лавуазье названо здесь не случайно. Во второй половине XVIII века развитие химии приостановилось. Талантливых химиков было по-прежнему достаточно техника химического эксперимента достигла такого совершенства, что многие достижения того времени используются до сих пор, - а наука стояла на месте. Лавуазье прежде всего обратил внимание на отсутствие ясности и единообразия в терминологии. При той путанице определений и понятий, которая царила в работах по химии, движение вперед было просто невозможно. С работ Лавуазье в химии началась пора расцвета.

В каком-то смысле Галуа сделал в математике то же, что Лавуазье в химии. Введение понятия группы избавило математиков от обременительной обязанности рассматривать множество различных теорий. Оказалось, что нужно лишь выделить «основные черты» той или иной теории, и так как, по сути дела, все они совершенно аналогичны, то достаточно обозначить их одним и тем же словом и сразу становится ясно, что бессмысленно изучать их по отдельности. «Здесь я занимаюсь анализом анализа». Эта мысль Галуа выражает его стремление внести в разросшийся математический аппарат новое единство. Теория групп - это прежде всего наведение порядка в математическом языке.

«Новые расположения» Паскаля , «номенклатура» Лавуазье , «группы» Галуа - все эти замечательные открытия снова и снова показывают, какую роль играет в науке установление новых связей. Каждое из этих открытий ознаменовало также значительное усовершенствование языка, используемого учёными».

Андре Дальма, Эварист Галуа: революционер и математик, М., «Наука», 1984 г., с. 44-49.